Fungsi Komposisi
Fungsi komposisi adalah “menggabungkan” sebuah fungsi ke dalam fungsi
lain sehingga menjadi fungsi baru (fungsi ketiga yang berbeda).Dalam definisi formal, jika ada fungsi f: X → Y, dan fungsi g: Y → Z, maka komposisinya bisa menjadi g ◦ f : X → Z, atau didefinisikan sebagai (g ◦ f )(x) = g(f(x)), untuk setiap x di X.
Operasi “g ◦ f” bisa disebut “g bundar f”, “g lingkaran f”, “g setelah f”, g dikomposisikan dengan f”, “g mengikuti f”, atau “g dari f”.
Untuk memudahkan pemahaman, bayangkan g(f(x)) sebagai fungsi g(x) yang variabel x-nya diganti dengan fungsi f(x).
Jika X = Y, maka f bisa dikomposisikan dengan dirinya sendiri menjadi f ◦ f = f2, yang disebut dengan “fungsi teriterasi”. Fungsi teriterasi dapat dinyatakan dengan ( f ◦ f) = f(f(x)) = f2(x), ( f ◦ f ◦ f)(x) = f3(x),
…, ( f ◦ f ◦ … ◦ f)(x) = f(f(…(f(x))…)) = fn(x), n disebut “pangkat fungsional” dari f.
P.S.: Ada banyak notasi alternatif yang digunakan untuk menyatakan operasi komposisi, namun hanya definisi standard di atas saja yang akan dipakai.
Sifat-sifat Fungsi Komposisi
- Asosiatif, artinya f ◦ (g ◦ h) = (f ◦ g) ◦ h.
- Operasi komposisi hanya bisa dijalankan ketika kodomain dari f merupakan subset dari domain g. (dalam kasus khusus, kodomain dari f = domain dari g.).
- Umumnya, operasi komposisi tidak selalu komutatif, artinya (g ◦ f) = (f ◦ g).
- Mempertahankan sifat injektif atau surjektif (atau bijektif) dari fungsi-fungsi yang dikomposisi, dengan asumsi bahwa kedua fungsi yang dioperasikan tepat injektif atau surjektif (atau bijektif) saja.
Contoh Fungsi Komposisi
- Untuk f: R → R dan g: R → R, di mana f(x) = 2x + 7 dan g(x) = x3, maka
(f ◦ g)(x) = f(g(x)) = 2x3 + 7.
- Jika ketinggian pesawat ada waktu t diberikan dengan fungsi h(t), dan konsentrasi oksigen pada ketinggian x diberikan dengan fungsi c(x), maka (c ◦ h)(t) = c(h(t)) (i.e. x = h(t)) adalah konsentrasi oksigen di sekitar pesawat pada waktu t.
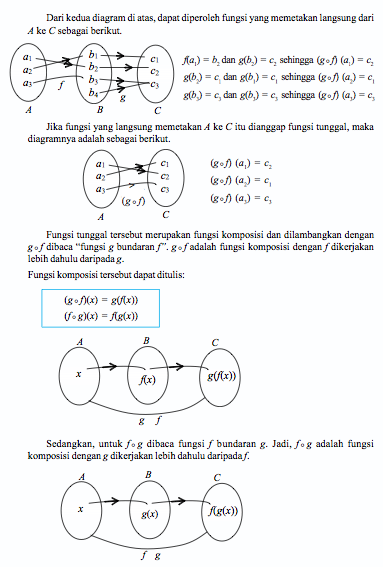
Nilai Fungsi Komposisi dan Komponen Pembentuknya
Untuk menjelaskan nilai fungsi komposisi terhadap komponen pembentuknya, dapat dilakukan dengan dua cara berikut ini.
- Dengan menentukan rumus komposisinya terlebih dahulu, kemudian disubstitusikan nilainya.
- Dengan mensubstitusikan secara langsung nilai pada fungsi yang akan dicari.
Untuk lebih memahami, perhatikan contoh soal berikut ini.
Contoh soal
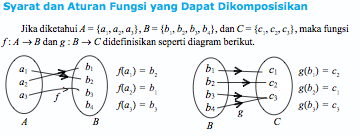
Diketahui
dua buah fungsi yang dinyatakan dengan rumus f(x) = 3x – 1 dan g(x) = x2
+ 4. Tentukanlah nilai dari fungsi-fungsi komposisi berikut.
a. (gcf)(1)
b. (f c g)(–2)
c. (gcf)(–3)
Penyelesaian
Cara 1
a. (g.0.f)(x) = g(f(x))
= g(3x – 1)
= (3x – 1)2 + 4
= 9x2–6x+1+4
= 9x2 – 6x + 5
(g.0.f)(1) = 9⋅12 –6⋅1+5
= 9–6+5=8
b. (f.0.g)(–2) = f(g(x))
= f(x2+4)
= 3(x2+4)–1
= 3×2+12–1
= 3×2+11
(f.0.g)(–2)
= 3(–2)2 + 11
= 3⋅4+11
= 12+11 = 23
c. (g.0.f)(x) = 9×2–6x+5
(g.0.f)(–3) = 9(–3)2 – 6 (–3) + 5
= 81+18+5
= 104
Cara 2a.(g.0.f)(1) = g(f(1))
= g(3⋅1–1)
= g(2)
= 22 + 4
= 8
b. (f.0.g) (–2) = f(g(–2))
= f((–2)2 + 4)
= f(8)
= 3⋅8–1 = 23
c. (g.0.f)(–3) = g(f(–3))
= g(3 (–3) – 1)
= g(–10)
= (–10)2 +4
= 104
Fungsi Invers
Fungsi Invers adalah fungsi yang “membalikkan” fungsi lain. Dengan
kata lain, jika f fungsi yang memetakan x ke ya, maka invers dari f,
yaitu f –1, kan memetakan y ke x.Sifat-sifat Fungsi Invers
- Unik/Tunggal, artinya untuk setiap f(x), jika ada 2 fungsi invers f1–1(x) dan f2-1(x) sedemikian sehingga f(f1-1(x)) = idx dan f(f2-1(x)) = idx, di mana idx adalah fungsi identitas, maka f1-1(x) = f2-1(x).
- Simetris, artinya untuk setiap fungsi f, maka f(f-1(x)) = f-1(f(x)) = idx = x, dan (f-1)-1 = f.
Contoh Fungsi Invers
- Misalkan f fungsi yang berbentuk y = f(x) = 13x + 19, maka x = f(y) = (y-19)/13, sehingga f-1(x) = (x-19)/13.
- Misalkan f fungsi yang memetakan/mengkonversi temperatur dalam skala Celsius ke skala Fahrenheit, i.e. F = f(C) = 9/5 C + 32.
Untuk sembarang fungsi f(x) dan g(x), maka (g ◦ f) -1 (x) = (f-1 ◦ g-1)(x) = f-1(g-1((x))).
Syarat agar Suatu Fungsi Mempunyai Invers
Semua himpunan yang dipetakan oleh fungsi
mempunyai invers. Invers dari himpunan tersebut dapat berupa fungsi
atau bukan fungsi. Perhatikanlah gambar di bawah ini.
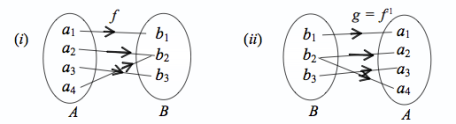
Dari gambar
(i), himpunan A yang beranggotakan (a1, a2, a3, a4) diperakan oleh
fungsi f ke himpunan B yang beranggotakan (b1, b2, b3) daerah hasil
adalah: {(a1, b1), (a2, b2), (a3, b3), (a4, b4)}. Pada gambar (ii)
himpunan B dipetakan oleh fungsi g ke himpunan A daerah hasil adalah:
{(b1, a1), (b2, a2), (b2, a4), (b3, a3)}. Pemetaan g : B → A diperoleh
dengan cara menukarkan atau membalik pasangan terurut f : A → B atau B
merupakan balikan dari f dinotasikan g = f-1, sering disebut g merupakan
invers dari f.
Menentukan Aturan Fungsi Invers dari Suatu Fungsi
Suatu fungsi
f akan mempunyai invers, yaitu f –1 jika dan hanya jika fungsi f
bijektif atau dalam korespondensi satu-satu. Misalkan, f merupakan
fungsi dari A ke B, maka f –1 merupakan fungsi invers f jika berlaku (f
–1 c f)(x) = x dan (f c f –1)(x) = x.
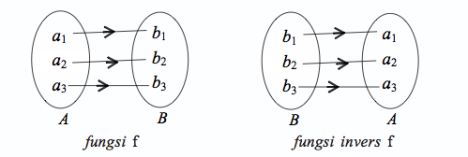
Perhatikanlah gambar di bawah ini.
Untuk menentukan fungsi invers dari suatu fungsi dapat dilakukan dengan cara berikut ini.
- Buatlah permisalan f(x) = y pada persamaan.
- Persamaan tersebut disesuaikan dengan f(x) = y, sehingga ditemukan fungsi dalam y dan nyatakanlah x = f(y).
- Gantilah y dengan x, sehingga f(y) = f –1(x).
Untuk lebih memahami tentang fungsi invers, pelajarilah contoh soal berikut ini.
Contoh soal
- Jika diketahui f(x) =, x≠-2 tentukan inversnya.
Penyelesaian
Misal f(x) = y, maka soalnya menjadi:
- Diketahui f : R → R dengan ketentuan f(x) = 3x + 8.
- Tentukan f–1(x).
- Tentukan (f–1 c f)(x).
- Tentukan (fcf–1)(x).
- Buktikan bahwa (f–1 c f)(x) = (f c f–1)(x).
Penyelesaian
SEKIAN...

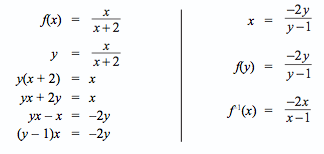
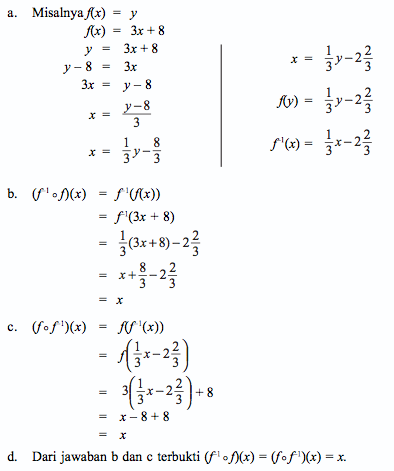







0 komentar:
Posting Komentar